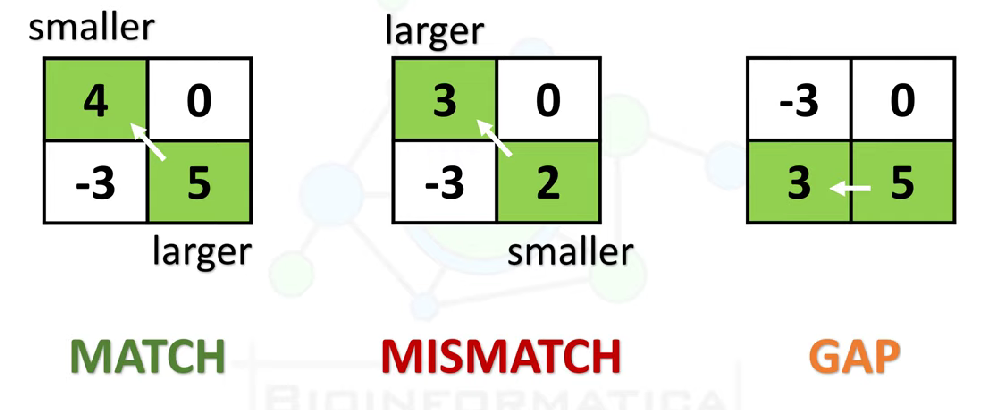
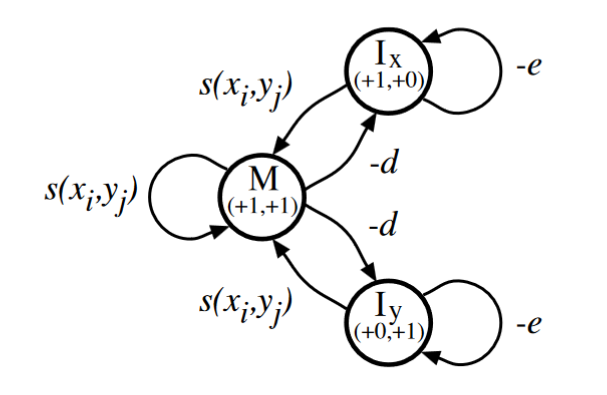
序列比对是什么以及序列比对主要的作用是什么,本篇博客就一笔带过,因为不是主要分享内容。 序列比对,此处引申为pairwise alignment会更加恰当一些,用于比较2条序列之间的相似程度,推断它们之间的相似程度,进而探索对应功能以及系统发育关系。 接下来大体分为2个部分,1)全局比对,2)局部比对 首先要明确一个概念:序列比对想要达到的目的是什么? 引一张图来说明序列比对的目的以及全局比对、局部比对之间的区别, 总的来说,也就是全局比对和局部比对想要达到的目的是不一样的, 利用动态规划来解决问题,最关键的一步就是列出动态规划公式,只要能列出公式,后面的编程也都只是时间问题。 但是,我并不想一上来就列出数学公式,我认为以一个简单的例子入手更有利于序列比对问题中的动态规划应用。 接下来,先理一理基于动态规划的序列比对的过程。 假设现在有2条长度分别为n、m的序列, 那则需要构建行数为n+1,列数为m+1的矩阵, 而“Filling”这个过程,即将第一列和第一行进行填充,从数学公式的角度来理解的话, 每一个单元的填充模式如下, 横向和竖向的移动代表了gap open(horizontal,vertical) 但更加复杂的情况应该考虑到gap在哪一条序列打开 对角线的移动则可以分为1)match(从大的数值回溯到小的数值),2)mismatch(从小的数值回溯到大的数值) Note:数值增大代表替换矩阵中,该碱基对应关系为match,而数值减小,代表替换矩阵中碱基对应关系为mismatch 出现4个单位长度的一个完整gap将两条序列给比对上,或者4个单位长度的单独gap将两条序列给比对上是更符合生物学原理的? 上述的文字情况如下所示, 答案是前者。这就需要在序列比对中引入另一个非常重要的细节 —— affine gap penalty。 Note:此处引入的affine gap penalty为“not penalize open with extension”,即在打开一个gap的时候,不会在该gap上同时引入open和extension的罚分 affine gap penalty,即在打开第一个gap的时候引入gap open罚分,而在该gap的基础上进行延续则采用gap extension罚分。 该种做法与原来的常量gap有一定区别,因此就需要改变动态规划公式,同时引入CS中的状态机可以帮助我们更好地理解这个问题。 上图中存在3个状态, 1)M:当前的比对情况下为match或mismatch 2)Ix:当前的比对情况为在seq2上打开一个gap,而seq1上为一个base 3)Iy:当前的比对情况为在seq1上打开一个gap,而seq2上为一个base 三者之间是可以相互转换的,通过d、e、s(x, y)来调整。 因此动态规划公式变为如下的形式,
但由于$$I_{x}$$在第一行以及$$I_{y}$$在第一列的取值都是不存在的,因此定义为-inf。 同时,由于每一个cell都存在一种情况,我们需要建立3个矩阵来存储对应的信息,分别用M、X、Y来表示。 经初始化之后,就可以得到如下3个矩阵: 代表在列方向打开一个gap,即seq2上插入一个gap 代表在行方向上打开一个gap,即seq1上插入一个gap 3个矩阵,可以使用1个矩阵来记录当前的cell的数值来源,3种情况如下 给个示例的回溯矩阵, 步骤与Global Alignment近似,只是引入了一个0,就可以得到局部的最佳匹配。 公式如下, [1] 《组学数据中的统计与分析》,田卫东 [2] https://users.soe.ucsc.edu/~karplus/bme205/f12/Alignment.html [3] https://www.youtube.com/watch?v=ZBD9he4Zp1E [4] Biological sequence analysis: Probabilistic models of proteins and nucleic acids

「步骤拆解」Global Alignment
(1)Intialization + Matrix Filling
(2)Tracing Back
「公式」Global Alignment
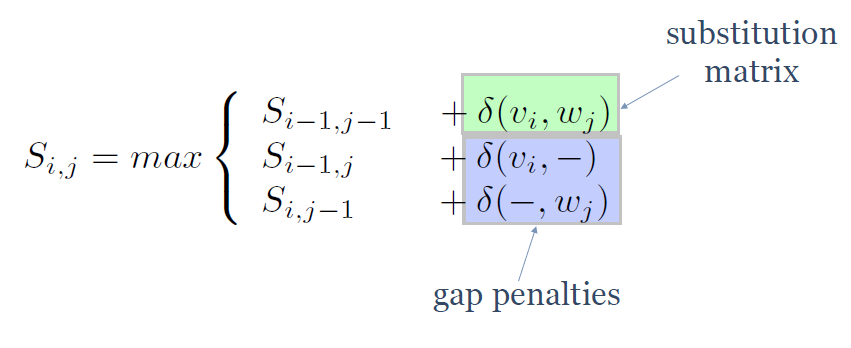
引入gap extension
# 1.
ATCGATCGATCGATCG----
AGCTAGCTCAGTACGT----
# 2.
ATCG-ATCG-ATCG-ATCG-ATCG
ATCG-ATCG-ATCG-ATCG-ATCG
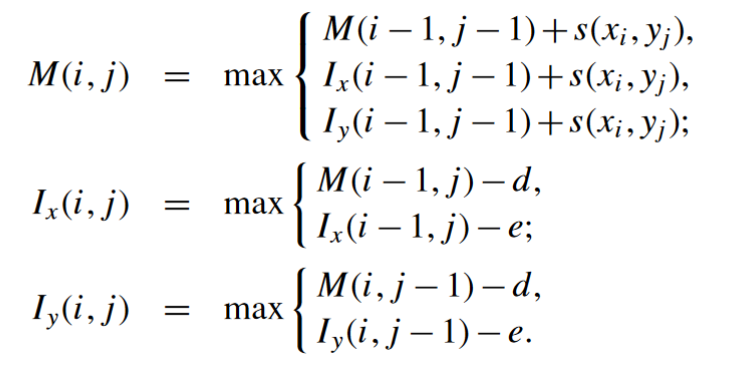
gap extension情况下的动态规划矩阵初始化
1)M
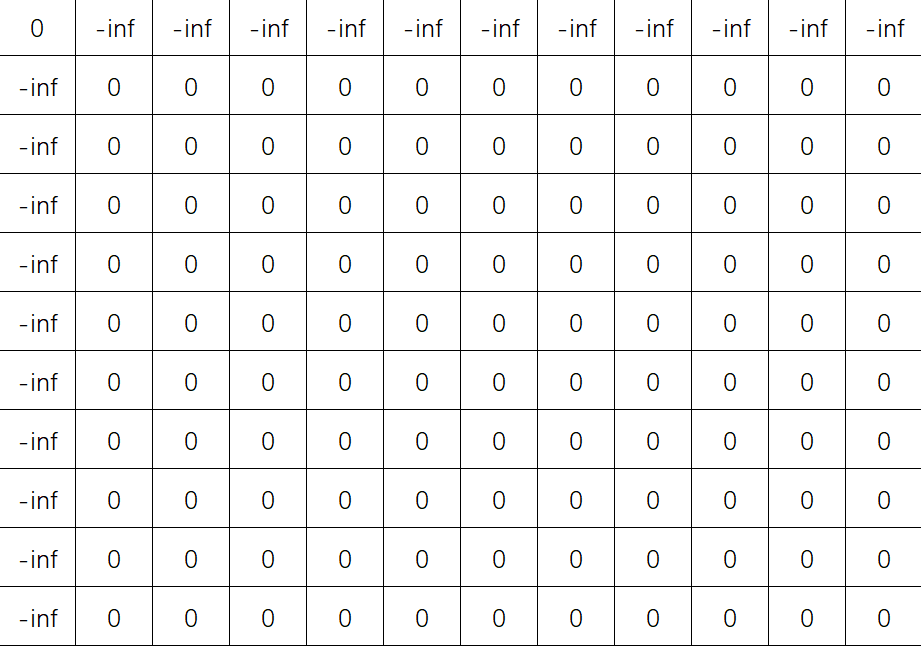
2)X
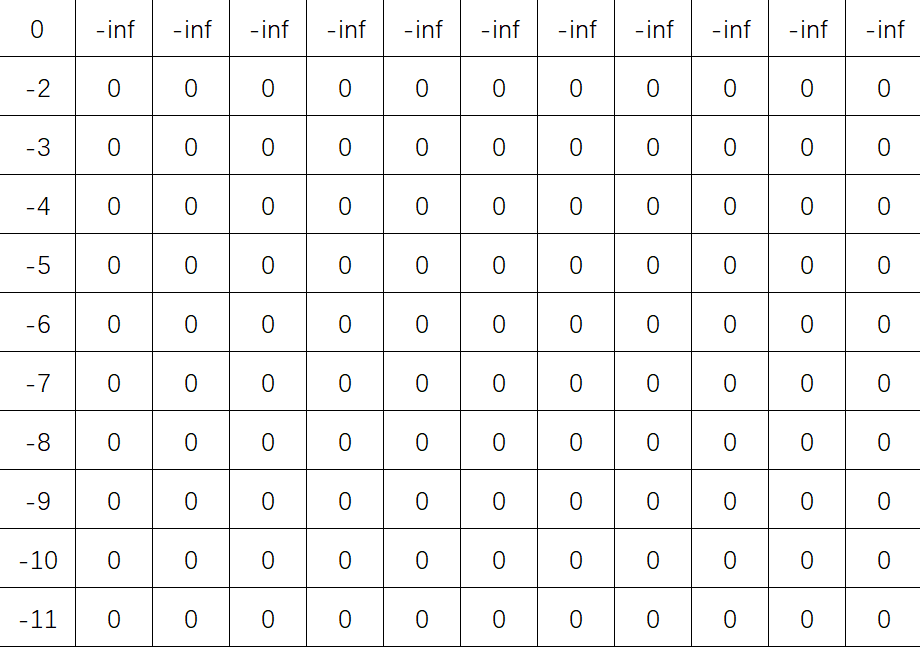
3)Y
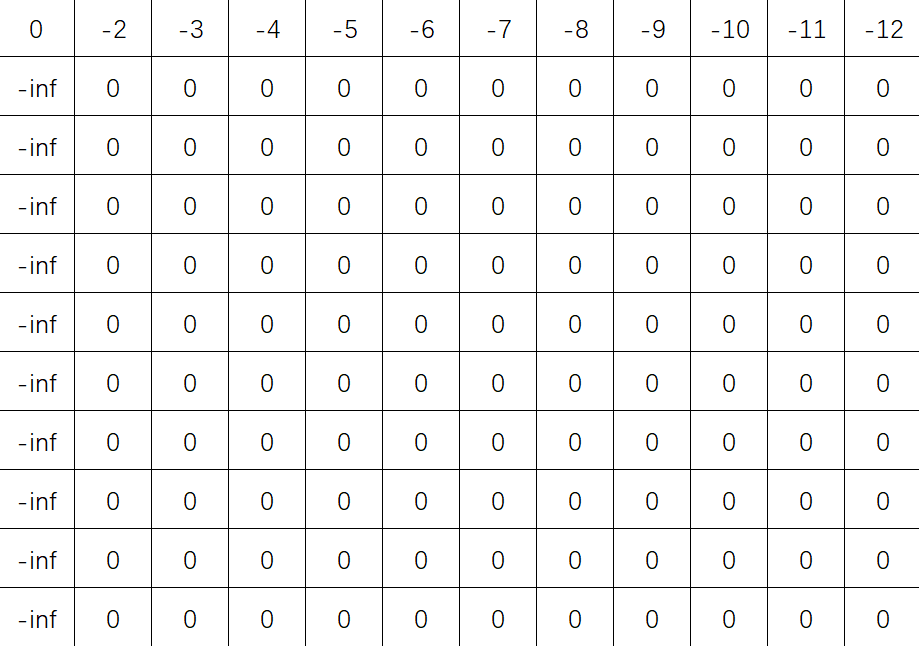
gap extension情况下的动态规划矩阵回溯

「步骤拆解」Local Alignment
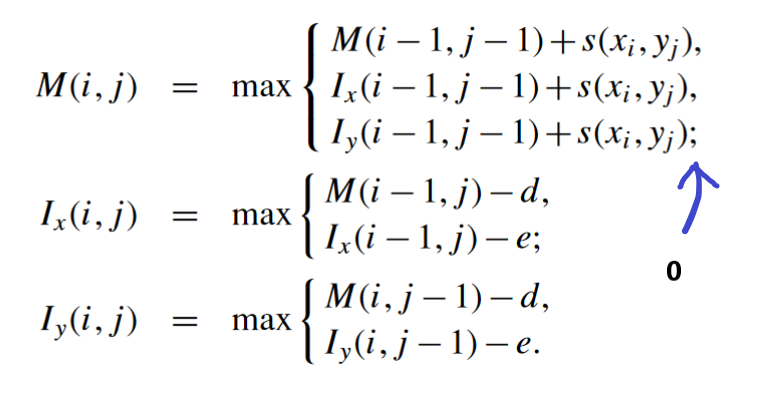
代码实现
import numpy as np
# Preset variables
seq1 = "TCGTAGACGA"
seq2 = "ATAGAATGCGG"
print(f'The seq1 has length of {len(seq1)}')
print(f'The seq2 has length of {len(seq2)}')
match = 1
mismatch = -1
gap_open = -2
gap_extension = -1
#
global MIN
MIN = -float("inf")
def identity_match(base1, base2):
'''Note: this function is used to compare the bases and return match point or mismatch point'''
if base1 == base2:
return match
else:
return mismatch
def createscorematrix(n, m):
'''Note: this function is used to generate the original score function'''
# Create match matrix, x matrix and y matrix
m_mat = [np.zeros(m+1) for i in range(0, n+1)]
x_mat = [np.zeros(m+1) for i in range(0, n+1)]
y_mat = [np.zeros(m+1) for i in range(0, n+1)]
return m_mat, x_mat, y_mat
m_mat, x_mat, y_mat = createscorematrix(len(seq1), len(seq2))
# print(m_mat)
# print(x_mat)
# print(y_mat)
def scorematrix_init(m_mat, x_mat, y_mat, d, e, local=False):
'''Note: this function conduct the score matrix initialization'''
'''Global Alignment'''
if local == False:
'''match matrix filling'''
for i in range(0, len(m_mat)):
for j in range(0, len(m_mat[0])):
if i == 0 and j == 0:
m_mat[i][j] = 0
elif i == 0 and j > 0:
m_mat[i][j] = MIN
elif i > 0 and j == 0:
m_mat[i][j] = MIN
# print(m_mat)
for line in m_mat:
r_list = [str(i) for i in line]
print(' '.join(r_list))
'''x_matrix filling'''
for i in range(0, len(x_mat)):
for j in range(0, len(x_mat[0])):
if i == 0 and j == 0:
x_mat[i][j]=0
if i > 0 and j == 0:
x_mat[i][j] = d+e*(i-1)
x_first_row = [0]
x_first_row.extend([MIN]*(len(x_mat[0])-1))
x_mat[0] = x_first_row
# print(x_mat)
for line in x_mat:
r_list = [str(i) for i in line]
print(' '.join(r_list))
'''y_matrix filling'''
for i in range(0, len(y_mat)):
for j in range(0, len(y_mat[0])):
if i == 0 and j == 0:
y_mat[i][j]=0
elif i > 0 and j == 0:
y_mat[i][j] = MIN
y_first_row = [0]
y_first_row.extend([d+e*(i-1) for i in range(1, len(y_mat[0]-1))])
y_mat[0] = y_first_row
# print(y_mat)
for line in y_mat:
r_list = [str(i) for i in line]
print(' '.join(r_list))
return m_mat, x_mat, y_mat
'''Local Alignment: Initialization step for Smith-Watermen is useless'''
if local == True:
return m_mat, x_mat, y_mat
m_mat, x_mat, y_mat = scorematrix_init(m_mat, x_mat, y_mat, -2, -1, local=False)
# m_mat, x_mat, y_mat = scorematrix_init(m_mat, x_mat, y_mat, -2, -1, local=True)
def matrix_filling(m_mat, x_mat, y_mat, d, e, local=False):
'''this function is used to create the scoring matrix using three dynamic programming,
and building a tracing matrix to restore the paths for the retrieve of aliignments'''
'''Global Alignment Activation'''
if local == False:
# Filling score matrix and record the trace
trace_matrix = [np.zeros(len(m_mat[0])) for i in range(0, len(m_mat))]
for i in range(1, len(m_mat)):
# print(m_mat[0])
for j in range(1, len(m_mat[0])):
# print(i, j)
m_mat[i][j] = max(
m_mat[i-1][j-1] + identity_match(seq1[i-1], seq2[j-1]),
x_mat[i-1][j-1] + identity_match(seq1[i-1], seq2[j-1]),
y_mat[i-1][j-1] + identity_match(seq1[i-1], seq2[j-1])
)
x_mat[i][j] = max(m_mat[i-1][j] + d, x_mat[i-1][j] + e)
y_mat[i][j] = max(m_mat[i][j-1] + d, y_mat[i][j-1] + e)
# for line in m_mat:
# print(line)
# Take the greatest values in these three matrix,
# merge into one matrix,
# and record the path
new_mat = [np.zeros(len(m_mat[0])) for i in range(0, len(m_mat))]
for i in range(0, len(m_mat)):
for j in range(0, len(m_mat[0])):
new_mat[i][j] = max(m_mat[i][j], x_mat[i][j], y_mat[i][j])
# Fill the trace matrix
# Note: from match/mismatch is 0, from x_mat (open a gap in seq2) is 1, from y_mat (open a gap in seq1)
if m_mat[i][j] == max(m_mat[i][j], x_mat[i][j], y_mat[i][j]):
trace_matrix[i][j] = 0
elif x_mat[i][j] == max(m_mat[i][j], x_mat[i][j], y_mat[i][j]):
trace_matrix[i][j] = 1
elif y_mat[i][j] == max(m_mat[i][j], x_mat[i][j], y_mat[i][j]):
trace_matrix[i][j] = 2
# # Print out the scoring matrix
# for line in new_mat:
# r_list = [str(i) for i in line]
# print('\t'.join(r_list))
# # Print out the tracing matrix
for line in trace_matrix:
r_list = [str(i) for i in line]
print('\t'.join(r_list))
return new_mat, trace_matrix
'''Local Alignment Activation'''
if local == True:
# Filling score matrix and record the trace
trace_matrix = [np.zeros(len(m_mat[0])) for i in range(0, len(m_mat))]
for i in range(1, len(m_mat)):
# print(m_mat[0])
for j in range(1, len(m_mat[0])):
# print(i, j)
m_mat[i][j] = max(
m_mat[i-1][j-1] + identity_match(seq1[i-1], seq2[j-1]),
x_mat[i-1][j-1] + identity_match(seq1[i-1], seq2[j-1]),
y_mat[i-1][j-1] + identity_match(seq1[i-1], seq2[j-1]),
0
)
x_mat[i][j] = max(m_mat[i-1][j] + d, x_mat[i-1][j] + e)
y_mat[i][j] = max(m_mat[i][j-1] + d, y_mat[i][j-1] + e)
# for line in m_mat:
# print(line)
# Take the Greatest values in these three matrix
new_mat = [np.zeros(len(m_mat[0])) for i in range(0, len(m_mat))]
for i in range(0, len(m_mat)):
for j in range(0, len(m_mat[0])):
new_mat[i][j] = max(m_mat[i][j], x_mat[i][j], y_mat[i][j])
if m_mat[i][j] == max(m_mat[i][j], x_mat[i][j], y_mat[i][j]):
trace_matrix[i][j] = 0
elif x_mat[i][j] == max(m_mat[i][j], x_mat[i][j], y_mat[i][j]):
trace_matrix[i][j] = 1
elif y_mat[i][j] == max(m_mat[i][j], x_mat[i][j], y_mat[i][j]):
trace_matrix[i][j] = 2
# # Print out the scoring matrix
# for line in new_mat:
# r_list = [str(i) for i in line]
# print(' '.join(r_list))
# # Print out the tracing matrix
# for line in trace_matrix:
# r_list = [str(i) for i in line]
# print('\t'.join(r_list))
return new_mat, trace_matrix
score_matrix, trace_matrix = matrix_filling(m_mat, x_mat, y_mat, -2, -1, local=False)
# score_matrix, trace_matrix = matrix_filling(m_mat, x_mat, y_mat, -2, -1, local=True)
# seq1 = "-TCGTAGACGA"
# seq2 = "ATAGAATGCGG"
def global_backtracking(matrix, score_matrix):
'''this function is used to trace back the input matrix and output the final alignment
Note: the input matrix is trace matrix'''
ti = len(seq1)
tj = len(seq2)
alignment1 = ''
alignment2 = ''
while (ti > 0 or tj > 0):
# Choose to go left, up or diagonal
cell = matrix[ti][tj]
if cell == 0:
alignment1 = seq1[ti-1] + alignment1
alignment2 = seq2[tj-1] + alignment2
ti -= 1
tj -= 1
elif cell == 1:
alignment1 = seq1[ti-1] + alignment1
alignment2 = '-' + alignment2
ti -= 1
elif cell == 2:
alignment1 = '-' + alignment1
alignment2 = seq2[tj-1] + alignment2
tj -= 1
# fmt_alignment = f'{alignment1}\n{alignment2}'
# print(fmt_alignment)
# Formt the info
info = f"======The Global======\n {alignment1}\n {alignment2}\nSCORE: {score_matrix[len(score_matrix)-1][len(score_matrix[0])-1]}"
print(info)
global_backtracking(trace_matrix, score_matrix)
def local_backtracking(trace_matrix, score_matrix):
'''this function does backtracking like FUNCTION global_backtracking, but in the way of local aligment'''
# Convert score matrix into Numpy array to find maximum value
new_score_matrix = np.array(score_matrix)
pos = np.unravel_index(np.argmax(new_score_matrix, axis=None), new_score_matrix.shape) # retrieve the maximum value
ti = pos[0]
tj = pos[1]
# print(f'{ti}\t{tj}')
alignment1 = ''
alignment2 = ''
while (ti > 0 or tj > 0):
if new_score_matrix[ti][tj] == 0: # stop local alignment back tracking when 0 values met
break
cell = trace_matrix[ti][tj]
if cell == 0:
alignment1 = seq1[ti-1] + alignment1
alignment2 = seq2[tj-1] + alignment2
ti -= 1
tj -= 1
elif cell == 1:
alignment1 = seq1[ti-1] + alignment1
alignment2 = '-' + alignment2
ti -= 1
elif cell == 2:
alignment1 = '-' + alignment1
alignment2 = seq2[tj-1] + alignment2
tj -= 1
info = f"======The Local======\n {alignment1}\n {alignment2}\nSCORE: {np.ndarray.max(new_score_matrix)}"
print(info)
# local_backtracking(trace_matrix, score_matrix)
参考文献
Hi,这里是有朴的第二大脑。
很高兴与你相遇
很高兴与你相遇