区分GWAS summary statistics中的是effect是odd ratio还是(即回归系数)时,需要考虑进来的一个因素: 经常看到的是为了logistic regression的方便求解 GWAS到底是针对binary phenotype开展的还是针对conitnuous phenotype开展的? 如果是针对binary phenotype,即case和control开展的,那么在构建回归模型来估计每个SNP对phenotype的影响时,使用的是logistic回归,最后计算的是一个阈值(概率),超过了即case,没有超过则是control。 logistic regression中的odd ratio是两个对立事件发生的概率做了一个比值: association test中的odd ratio是基于列联表的计算,两种方法的计算本质实际上是一样的:
斯坦佛大学这张slides解释的非常清晰:首先计算odd,再计算odd ratio 比如genotype AT出现的情况下,individual患病的概率是0.8。这是一个明显的条件概率问题。而当genotype TT出现的情况下,individual患病的概率则是0.2。 从这里其实就可以观察到不同的genotype对individual是否有对应disease的susceptability是不同的,但是如何量化?答案即odd ratio。 针对同一个genotype,其出现的情况下,患病和不患病之间的差距是多大?
针对两个genotype,患病和不患病之间的差距有多大?
上述的概率,在logistic regression是可以直接拟合出来的。但是在association test中实际上一样, 下述计算odd ratio的意义是为了比较C allele相较于T allele对disease occurrence的影响, 而这个式子()可以拆开看:Odd Ratio和|logistic & linear

Odd Ratio|计算原理

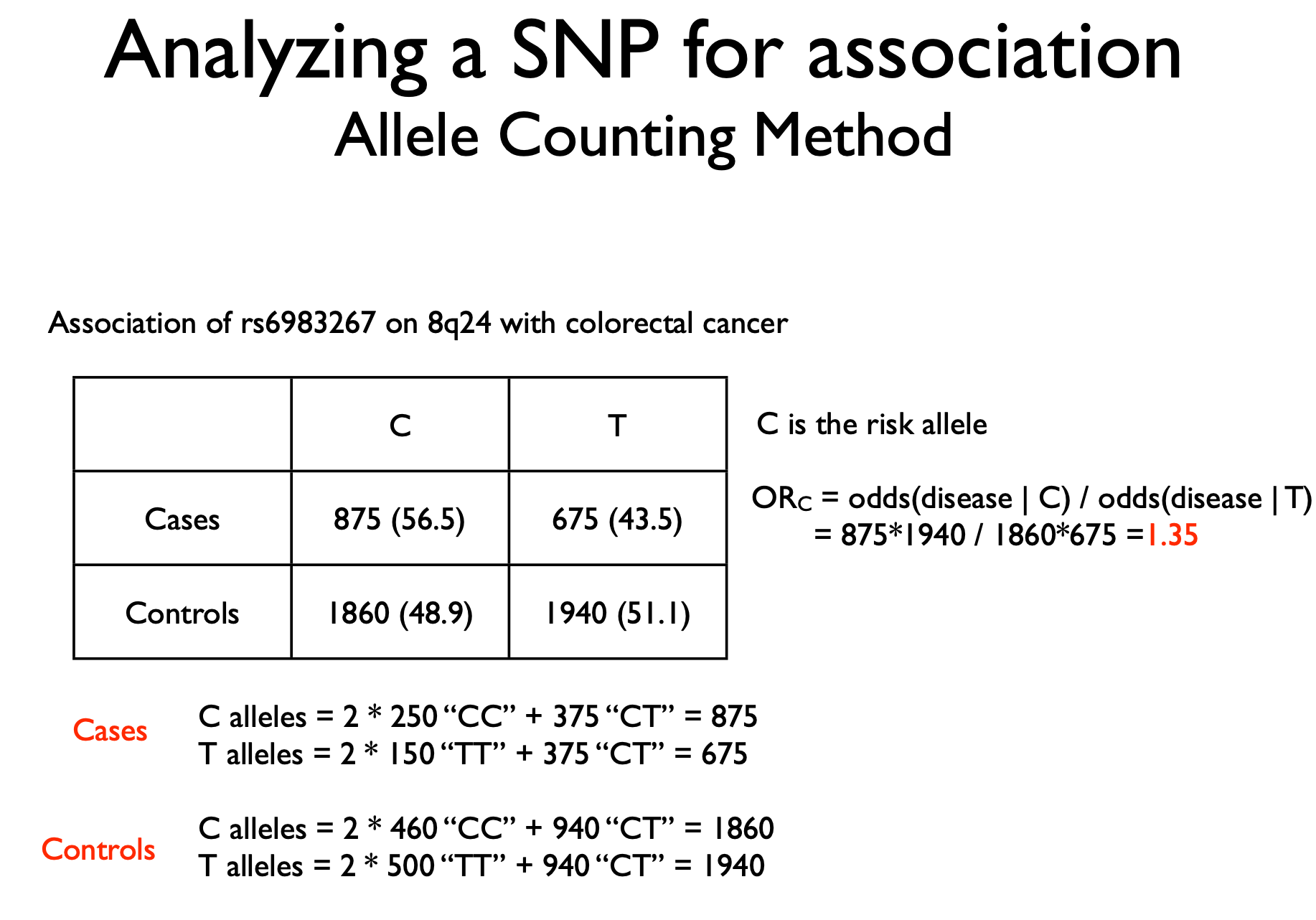
参考资料
Hi,这里是有朴的第二大脑。
很高兴与你相遇
很高兴与你相遇