Wright提出的FST原始版本,并没有考虑到sample size对计算的影响,因此才有了之后Weir and Cockerham对计算的改进。 而在展开介绍Weir和Cockerhem是如何计算之前,先看看Wright是如何计算, θ,即指代。 在WC estimator中,其计算公式如下, Note:该版本计算得到的FST,与vcftools略有不同,尚且认为是自己写作了吧。 但是上述文献中最终给出的,也仅仅是FST的最终计算公式,没有给出一个更加详尽的推导。 如下的理解来自02年Weir发表对应文献/tutorial。 首选需要阐明的几个点, 1)假设现在一个sample中,第j个allele,若其碱基类型为μ,则等于1;若其碱基类型不为μ,则等于0。用来表示, 那么现在针对期望population allele frequency为如下的形式, Note:此处公式存在一点问题(个人角度),应该论述为 ε,代表
当,则,但是因为两者不相等,所以需要用θ来平衡他们之间的关系,而从生物学意义的角度来理解, 若第j位和第j'位之间,完全不存在联系,完全不可能是IBD,则 若第j位和第j'位之间,在一定程度上是IBD,则需要接着考虑θ。 2)但是现在不从一个sample的角度考虑,而是从2个population之间的角度考虑, Note:若前提为non-random mating,则说明两个群体之间存在了divergence、isolation等 因此,此时的进一步引申为了衡量population differentiation的指标。 而针对sample allele frequency则由如下的公式计算得到, 且由于不同population size,抽样得到的sample计算出来的存在偏差(Nicolas提出其服从参数为的正态分布) 而Weir于1984年提出的Weighted ,为了消除不同population size对衡量的影响,构建了如下的两个平方差, 最终则表示为, Note:我看了很久还是没看懂。。得再看看 用bedtools + R tidyverse来计算每个gene的FST忒慢了(这怎么“Have a nice day”),欢迎有缘人后台留言优秀方法!Weir and Cockerham | Weighted 计算公式
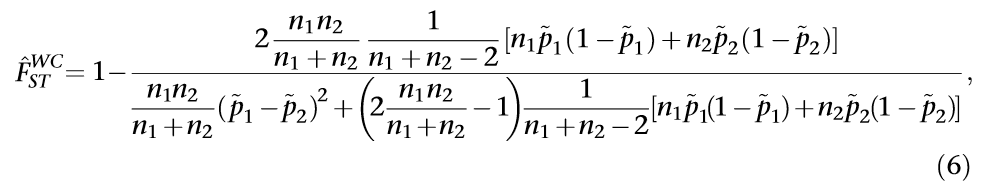
Weir | 推导
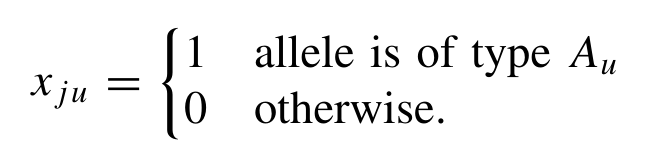

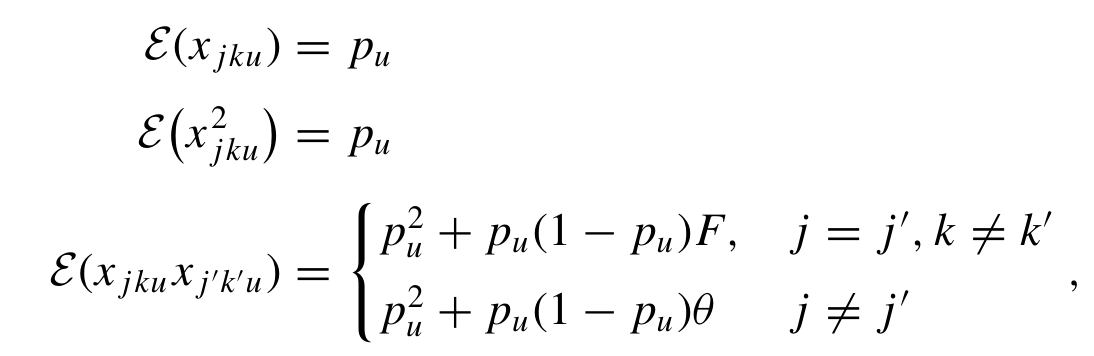
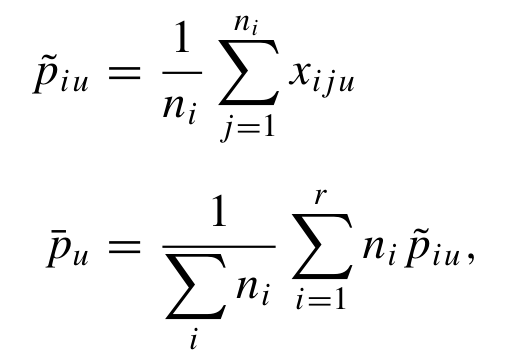
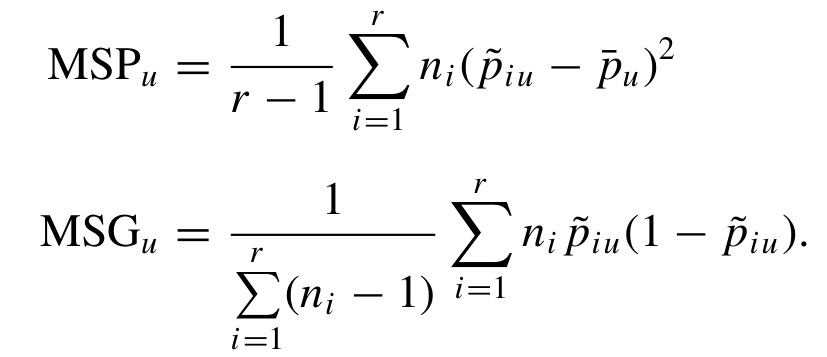
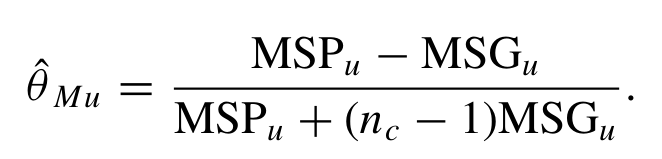
推荐阅读
题外话
Hi,这里是有朴的第二大脑。
很高兴与你相遇
很高兴与你相遇