无性繁殖群体的特征,即offspring,子代个体的genotype与祖先代相同。 现假设群体中存在2种strain,即两种genotype不同的亚群体,设为1和2, 再给定如下的一些参数, 即可以得到下一代的对应strain的数量如下, 那么在代中,strain 1和strain2的种群数量分别为,
而第t+1个generation和第t个generation中不同strain的种群数量比例,可以表示为,
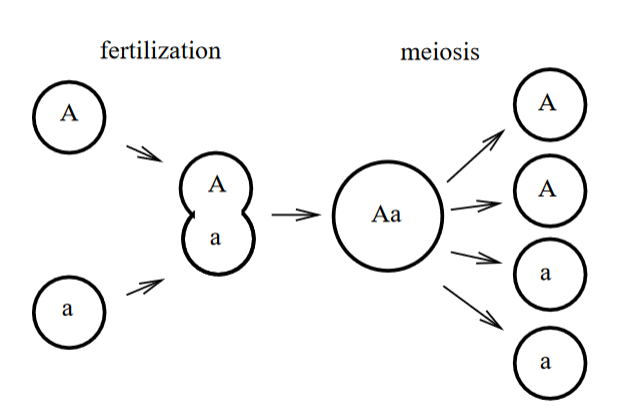
重要推论:每一种strain在群体中的种群数量占比,是不变的, 上述情况拓展到,i个strain,也是一样的, 每一个strain的占比, 以下面这个species为例(e.g. 一般是微生物具有类似的生殖模式,即haploid-> diploid -> haploid,如下图),现假设群体中存在两种genotype A和a。不同于二倍体,haploid物种,在单个locus只存在一个allele,要么是A,要么是a。 那么在当前这一代,能够形成如下的几种genotype的二倍体,其frequency(genotype frequency)如下, 下一代中对应genotype的haploid个体所对应的frequency如下, Note:上述即为HW equilibrium,其有一个非常重要的假设,即infinite population,而这又可以进一步推导出每一种genotype可以产生的子代数量是一致的,如下,
现假定一个存在二倍体群体,且某一条常染色体上存在两个可进行segregating(服从孟德尔分离定律)的allele,同时这个群体中不同性别中的genotype frequency需要相同, Note:这个前提非常重要喔,在后续进一步理解sex-linked locus的gene frequency equilibrium非常有用 比如female population中,Aa genotype frequency=0.7,male population中,Aa genotype frequency也要为0.7,即不考虑群体数量对mating的影响,用公式来表示,
总结一下,该diploid population需要满足的前提, 而 这样的群体,在经过一代的随机交配之后,即可达到Hardy-Weinberg equilibrium, 同时需要注意的是, “Mendelian reproduction in a random mating population has no inherent tendency to favor one allele or the other.” 上面这句话就对应了“genotype frequency -> 常量”这个结果,即孟德尔遗传只是一种本质上的规律,是机制,而真正能够改变gene frequency的驱动力,是natural selection和genetic drift。 这个问题就比如将二分类问题推广到多分类问题,本质上是一样的。 之前讨论的模型,都是建立在每一代每一代完全分隔,群体中的每一个个体都知道,“爷今天出生了”、“爷明天要死了”的情况,大家出生和死的时间都是非常一致的,但是真实的情况应该是,“我先逝了,你慢点逝”等。 数学语言怎么建立? 每一代随机选择一部分的个体去“逝世”,并被新的individual所取代,该比率为; 对一个个体来说,其能够存活t个单位时间的概率如下,
,为单次存活下来的概率 ,为逃过一劫的次数 以genotype AA为例, 那我们就可以列出下面的公式,即单位时间内AA genotype的变化幅度,
变化形式之后可以得到,
为了后续进行定积分,我们进一步转换,得到下列的式子,
为了解开上述的式子,解出C的值非常重要,可以通过设定t=0,来进行求解,即。 进一步转化得到,
对数转换之后且转换之后,可以得到最终的式子,
当t趋近于∞的时候,,即达到Hardy-Weinberg equilibrium 现假定female population中,A gene frequency为,male population中为, generation之间的计算规律如下, 下一代中,female、male population中的A gene frequency为,
从t generation到t+1generation,父母本都只有一半的gametes可以传递下来,对应式子中的1/2 diploid population,且同时引入了sex differentiation的情况,无法通过一代达到Hardy-Weinberg equilibrium, 即t+1代中的,不等于该代的 这种情况有一个非常重要的前提:该sex-linked locus位于X chromosome上,且Y chromosome上没有对应的同源区段。 同样的假设,female population中,A gene frequency为,male population中为, 那么即可以得到在t+1 generation的female population中,3种genotype分别对应的频率为, 带入上一个部分的公式,可以得到female population中A gene的frequency,为。 在male population中,对应的genotype frequency为, 而对于male来说,A gene frequency即为。 这还远远没有达到平衡,那么平衡时的公式如何呢?
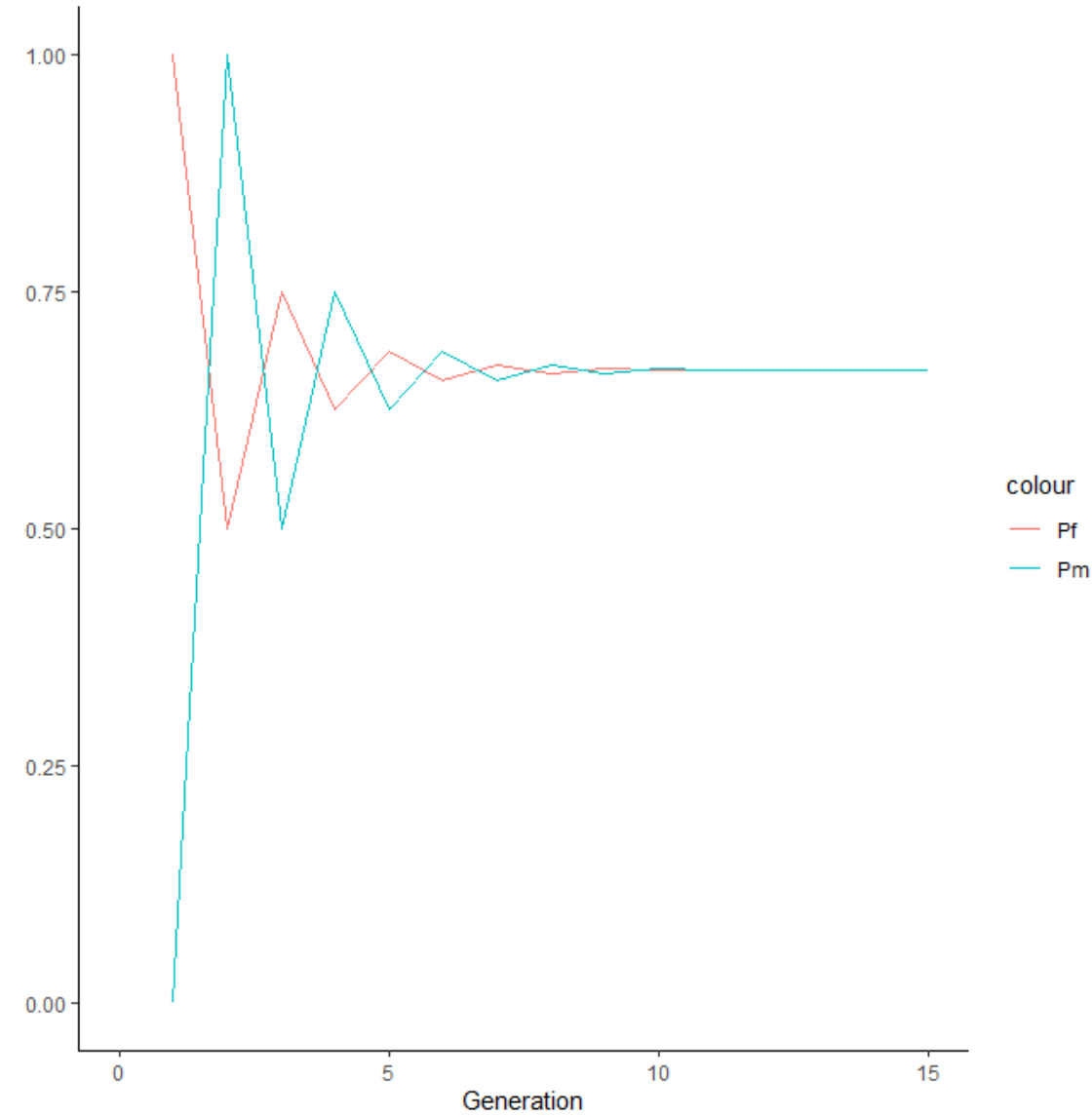
我的代码, 当的初始情况下,在0.667收敛,如下图,
导入 | 以asexual inheritance和haploid inheritance为例
Asexual inheritance
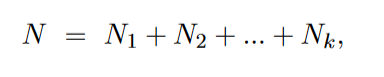
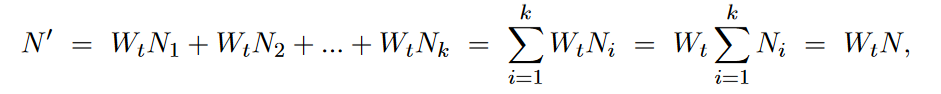
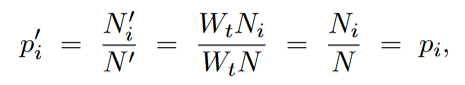
Haploid inheritance
HW equilibrium的引入
Diploid with two alleles
Multi-alleles的情况一样吗?
群体动态变化 | Overlapping generations的引入
怎么体现genotype frequency随时间变化而变化?
从这个式子,可以得出什么结论?
性别的不均匀贡献 | sex-linked locus的引入
sex differentiation的引入
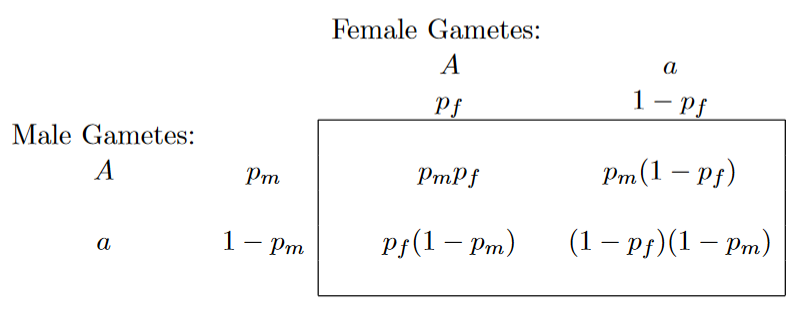
从这个式子,可以得出什么结论?
sex-linked locus的引入
来几道题 | 起始分别为(1,0), (0,1), (0.5, 0.5)的情况下,最终群体的A gene frequency在什么数值收敛?
pf <- 1; pm <- 0
# pf <- 0; pm <- 1
# pf <- 0.5; pm <- 0.5
generation.vector <- c(pf, pm)
# simulate the pf and pm in 200 loops
for (i in seq(3, 150, by = 2)){
tmp.pf <- (generation.vector[i-2] + generation.vector[i-1]) / 2
tmp.pm <- generation.vector[i-2]
generation.vector <- c(generation.vector, tmp.pf, tmp.pm)
}
length(generation.vector)
# retrieve the pf and pm
pf.vector <- c()
pm.vector <- c()
for (i in seq(1,150, 2)) {
pf.vector <- c(pf.vector, generation.vector[i])
}
for (i in seq(2,150, 2)) {
pm.vector <- c(pm.vector, generation.vector[i])
}
p.dat <- data.frame("Pf"=pf.vector, "Pm"=pm.vector, "Generation"=seq(1:75))
tail(p.dat)
# plot(p.dat$Pf)
# plot(p.dat$Pm)
library(ggplot2)
p <- ggplot(data = p.dat, aes(x = Generation)) +
geom_line(aes(y = Pf, color = "Pf")) +
geom_line(aes(y = Pm, color = "Pm")) +
theme_classic() +
scale_y_continuous(limits = c(0, 1)) +
scale_x_continuous(limits = c(0, 15)) +
ylab("")
p
# ggsave("sim-HWprinciple-sex-linked-locus.pdf", p, height = 6, width = 10)
其他
公式推导 |
Hi,这里是有朴的第二大脑。
很高兴与你相遇
很高兴与你相遇